Timing Inaccessibility and the Projection Bound: Resolving Maxwell's Demon for Continuous Biological Substrates

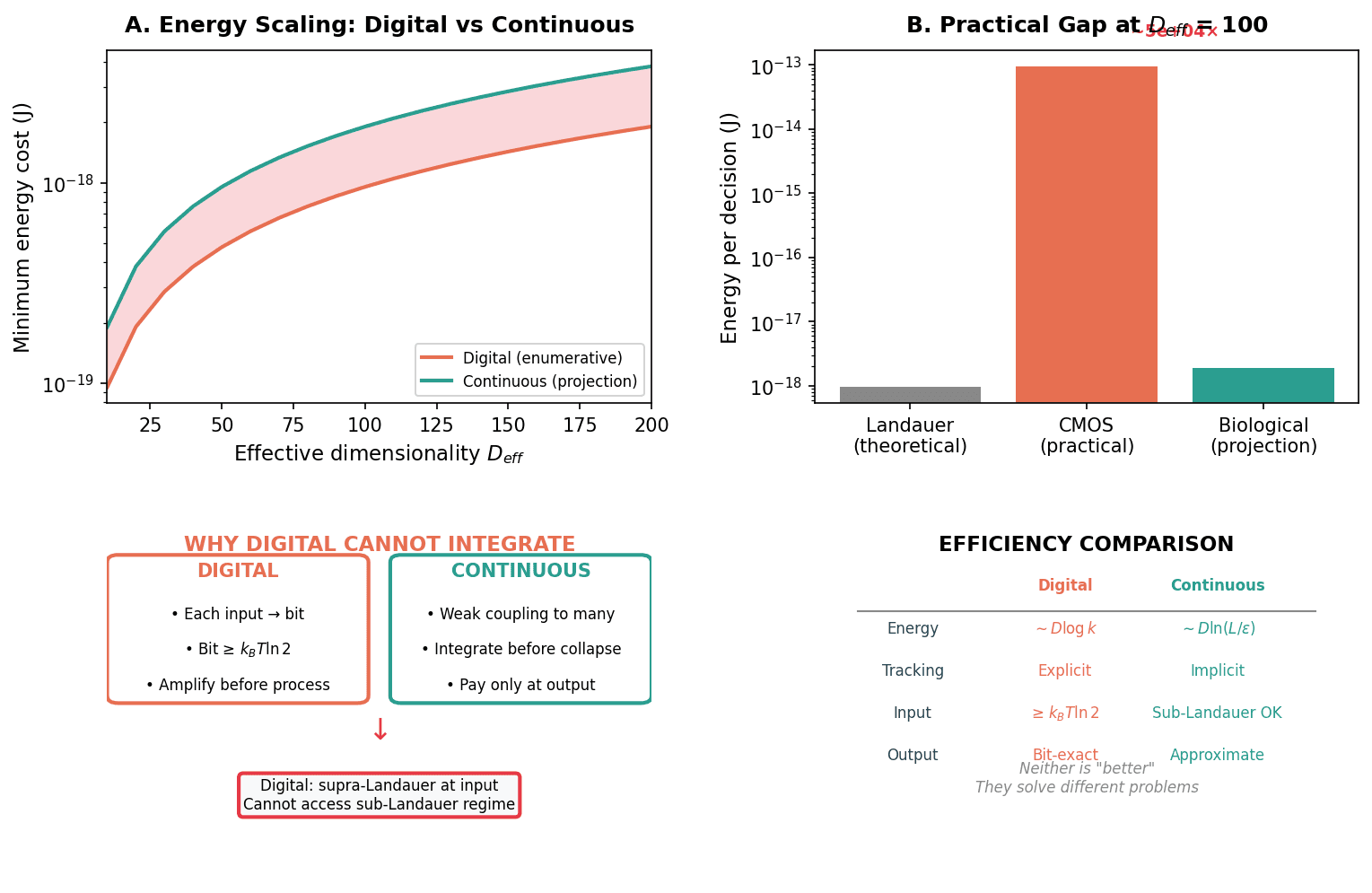
The brain is 100,000× more energy-efficient than silicon because it defers thermodynamic costs — computing reversibly until the moment it must commit to a discrete output.

Version 2.0 now available

v2.0 (December 2025) extends the published paper with three new arguments: (1) Framework dependence of timing — what counts as "simultaneous" vs "sequential" depends on the measurement framework, making temporal structure framework-relative. (2) The "when" is created, not revealed — temporal order does not pre-exist measurement but emerges at projection. (3) AI substrate constraints — digital architectures cannot access the sub-Landauer integration regime regardless of scale, though behavioral approximation may remain possible.

The paper now explicitly traces the Maxwell's demon lineage (Maxwell → Szilard → Landauer → Bennett → this paper), showing how biological systems extend the resolution to continuous substrates via path degeneracy. The key insight: the Landauer-Bennett resolution assumed discrete memory states; biology operates with continuous dynamics where "memory" is structural correlation, not written bits.

Below the Landauer limit ($\sim 3 \times 10^{-21}$ J), you can't irreversibly record when things happen without paying $\ge k_BT\ln 2$ per stabilized order bit. This creates massive "path degeneracy" — exponentially many micro-trajectories ($10^{50}$ to $10^{100}$ in neural systems) that all look the same from the outside. Biology exploits this via a two-stage model: Stage 1 (reversible correlation) is thermodynamically cheap; Stage 2 (stabilization/projection) is where the cost appears.